Hôm nay tôi chia sẻ với các bạn một nội dung thường gặp trong quá trình xây dựng các mô hình trong tài chính- đó chính là việc bỏ sót biến trong quá trình mô hình. Đây là một lỗi thường gặp, và nó dẫn đến hậu quả nghiêm trọng cho việc sử dụng các kết quả của hồi quy để thực hiện việc dự báo.

Trong quá trình xây dựng mô hình hồi quy, một số bạn gặp phải khó khăn trong việc lựa chọn các biến giải thích (explanatory variables) để đưa vào mô hình sao cho phù hợp. Cụ thể hơn, hai vấn đề các bạn thường mắc phải là (1) đưa quá ít các biến dẫn đến hiện tượng bỏ sót biến quan trọng (omitted variables) hoặc (2) đưa quá nhiều các biến dẫn đến có những biến là không phù hợp (irrelevant variables) trong mô hình. Đầu tiên mình sẽ nói về vấn đề bỏ sót biến.
Những vấn đề gặp phải khi bỏ sót biến
Nếu các biến có ý nghĩa trong việc giải thích sự vận động của biến kết quả hay còn gọi là biến phụ thuộc (dependent variable) vắng mặt trong mô hình nghiên cứu sẽ dẫn đến các hệ số hồi quy ước lượng theo phương pháp OLS (bình phương nhỏ nhất) của các biến giải thích/nguyên nhân có trong mô hình bị thiên lệch (bias).
Nguyên nhân thường dẫn đến việc bỏ sót biến là do các lý thuyết liên quan chưa có cái nhìn đầy đủ về vai trò của một biến số nào đó hoặc cũng có thể do sự hạn chế về mặt dữ liệu trên thực tế (dữ liệu không có sẵn) dẫn đến việc chúng ta bỏ qua biến số này trong mô hình.
Ví dụ: Giả sử chúng ta muốn xây dựng một mô hình dự báo thu nhập của một hộ gia đình (FAMINC), biến giải thích cho mô hình là số năm đi học của chồng (HEDU) và số năm đi học của vợ (WEDU). Thực tế hiện nay cả vợ và chồng đều tham gia lao động để tạo ra thu nhập nên hai biến giải thích đưa vào mô hình là hợp lý. Chúng ta có kết quả hồi quy như sau:
Nhìn vào kết quả, các bạn có thể giải thích ý nghĩa hệ số hồi quy đối với biến HEDU là nếu số năm học của người chồng tăng hoặc giảm một năm, các biến số khác không đổi, thì kỳ vọng thu nhập của gia đình tăng hoặc giảm 3132 USD.
Giả sử như chúng ta bỏ sót biến trình độ học vấn của người vợ, chúng ta có kết quả hồi quy như sau:
Nhìn vào kết quả hồi quy ta thấy, nếu số năm đi học của người chồng tăng hoặc giảm một năm thì sẽ làm cho thu nhập của gia đình kỳ vọng tăng hoặc giảm 5155 (USD).
Như vậy, việc bỏ sót một biến quan trọng là WEDU dẫn đến chúng ta đánh giá vai trò của biến HEDU trong việc tác động đến thu nhập cao hơn thực tế khoảng 2000 USD (Đây là mức độ thiên lệch).
Qua ví dụ trên chúng ta thấy được hậu quả đối với việc bỏ sót biến là rất nghiêm trọng, sai phạm này ảnh hưởng trọng yếu đến việc diễn dịch các kết quả của mô hình, khả năng dự báo của mô hình.
Mức độ sai lệch sẽ được tính theo công thức như sau:
Giả sử mô hình hồi quy tổng quát là:
Giả sử chúng ta bỏ sót biến x3 là một biến số có ý nghĩa trong việc giải thích cho sự biến động của biến y. Lúc này, mô hình chỉ còn:
Mức độ thiên lệch sẽ tính như sau:
Chẩn đoán bỏ sót biến
Bạn có thể sử dụng một số cách sau để chẩn đoán việc bỏ sót biến:
a. Sử dụng Adjusted R2
Dấu hiệu rõ nhất cho việc các biến giải thích đang bị bỏ sót biến là Adjusted R2 thấp (thế nào gọi là thấp, điều này phụ thuộc vào đặc thù từng ngành, từng lĩnh vực nghiên cứu, điều này mình sẽ trao đổi với các bạn trong một nội dung khác). Tuy nhiên, việc Adjusted R2 thấp có thể là do việc chọn lựa sai dạng hàm (ví dụ như bài toán chúng ta có dạng hàm phi tuyến nhưng chúng ta lại chọn hàm tuyến tính), vì vậy đôi khi bạn thực sự có tất cả các biến phù hợp trong mô hình rồi nhưng vẫn cho kết quả Adjusted R2 thấp.
b. t-values
Nếu biến bỏ sót đã biết và có sẵn dữ liệu đo lường bạn có thể đưa biến này vào mô hình và kiểm tra giá trị thống kê t của nó. Nếu giá trị thống kê t là cao (mức ý nghĩa nhỏ) thì chúng ta có thể kỳ vọng nên đưa biến này vào mô hình.
c. Sử dụng kiểm định RESET (Regression Specification Error Test) của Ramsey
Trong nghiên cứu của Ramsey (1969) đề suất việc lấy mũ các ŷ (là giá trị dự báo của biến độc lập, tính từ mô hình hồi quy) (ví dụ như ŷ2, ŷ 3 và ŷ 4) như là các giá trị đại diện cho các biến z bị bỏ sót (chưa biết).
Quy trình kiểm định RESET như sau:
B1: Hồi quy biến phụ thuộc y với biến giải thích đã biết là x:
y = b1 + b2x (1)
Từ mô hình hồi quy (1) ta tính các giá trị dự báo ŷ.
B2: Hồi quy y với các biến x, ŷ 2, ŷ 3 và ŷ 4:
y = g1 + g2 x + g3 ŷ 2 + g4 ŷ 3 + g5 ŷ 4
B3: Thực hiện kiểm định F cho giả thuyết liệu các hệ số hồi quy của ŷ 2, ŷ 3 và ŷ 4 đều bằng Zero hay không.
H0: g3=g4=g5=0
H1: ít nhất một trong ba giá trị g3, g4, g5 khác 0
Nếu chúng ta bác bỏ giả thuyết H0 thì đó là bằng chứng cho việc bỏ sót biến.
Giải pháp cho việc bỏ sót biến
Giải pháp rõ ràng nhất là đưa các biến có thể vào mô hình nếu chúng có sẵn (data). Nếu không, chúng ta có thể sử dụng các giá trị đại diện cho các biến này (đòi hỏi việc xây dựng một biến quan sát thay thế). Nhiều bạn cho rằng, như vậy thì tốt nhất là chúng ta cứ đưa càng nhiều biến vào mô hình càng tốt vì sẽ tránh được hiện tượng bỏ sót biến, việc đưa “thừa” các biến không quan trọng vào mô hình không gây ra hiện tượng thiên lệch đối với các ước lượng OLS cho các hệ số hồi quy, nhưng các bạn nên cẩn thận điều này vì việc đưa thừa biến sẽ dẫn đến một số vấn đề khác trong kết quả hồi quy (điều này sẽ được nói ở một nội dung khác).
___________________________________
Tài liệu tham khảo
Hill, R. C., Griffiths, W. E., & Lim, G. C. (2008). Principles of econometrics (Vol. 5): Wiley Hoboken, NJ.
Ramsey, J. B. (1969). Tests for specification errors in classical linear least-squares regression analysis. Journal of the Royal Statistical Society. Series B (Methodological), 350-371.











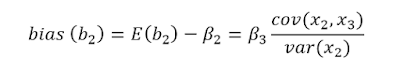












0 nhận xét:
Đăng nhận xét