Mô hình tự phân phối độ trễ Hồi quy ARDL
Mô hình tự phân phối độ trễ Hồi quy ARDL ( Autoregressive distributed lag model); Đây cũng là một mô hình dự báo kinh tế quan trọng được áp dụng nhiều trong kinh tế, với kết quả gần giống với mô hình vectơ hiệu chỉnh sai số, nhưng nó mạnh mẽ hơn ở chỗ sẽ tự động phân phối độ trễ (lag), nhưng lại không có thể phân tích phản ứng đẩy – cú shock như mô hình VAR; Mỗi một model định lượng thì sẽ có những ưu và nhược điểm riêng.
HỒI QUY ARDL
Hồi quy ARDL là gì ?
Mô hình độ trễ phân tán tự động hồi phục, trong đó biến phụ thuộc là một hàm của các giá trị trễ trong quá khứ của chính nó cũng như các giá trị hiện tại và quá khứ của các biến giải thích khác.
Trong thống kê và kinh tế lượng , mô hình độ trễ phân tán là một mô hình cho dữ liệu chuỗi thời gian , trong đó phương trình hồi quy được sử dụng để dự đoán các giá trị hiện tại của một biến phụ thuộc dựa trên cả giá trị hiện tại của một biến giải thích và các giá trị bị trễ (giai đoạn quá khứ) của biến giải thích này.
Mở rộng mô hình tự phân phối độ trễ
Trong mô hình độ trễ phân tán vô hạn, cần ước lượng vô số trọng số độ trễ; rõ ràng điều này chỉ có thể được thực hiện nếu một số cấu trúc được giả định cho mối quan hệ giữa các trọng số trễ khác nhau, với toàn bộ tính vô hạn của chúng có thể biểu thị được dưới dạng một số lượng hữu hạn các tham số cơ bản giả định.
Trong mô hình độ trễ phân tán hữu hạn, các tham số có thể được ước tính trực tiếp bằng bình phương nhỏ nhất thông thường (giả sử số lượng điểm dữ liệu đủ lớn hơn số trọng số độ trễ); tuy nhiên, ước lượng như vậy có thể cho kết quả rất không chính xác do đa cộng tuyến cực độ giữa các giá trị trễ khác nhau của biến độc lập, do đó, một lần nữa có thể cần giả sử một số cấu trúc cho mối quan hệ giữa các trọng số trễ khác nhau.
Phân loại hồi quy ARDL
Mô hình trễ phân tán có cấu trúc có hai loại: hữu hạn và vô hạn. Độ trễ phân phối vô hạn cho phép giá trị của biến độc lập tại một thời điểm cụ thể ảnh hưởng đến biến phụ thuộc vô hạn trong tương lai, hoặc nói một cách khác, chúng cho phép giá trị hiện tại của biến phụ thuộc bị ảnh hưởng bởi các giá trị của biến độc lập điều đó đã xảy ra cách đây vô cùng lâu; nhưng vượt quá một số độ trễ, các hiệu ứng giảm dần về 0. Độ trễ phân phối hữu hạn cho phép biến độc lập tại một thời điểm cụ thể ảnh hưởng đến biến phụ thuộc chỉ trong một số khoảng thời gian hữu hạn.
Độ trễ phân phối vô hạn
Mô hình trễ phân tán hữu hạn có cấu trúc quan trọng nhất là mô hình trễ Almon . Mô hình này cho phép dữ liệu xác định hình dạng của cấu trúc độ trễ, nhưng nhà nghiên cứu phải xác định độ dài độ trễ tối đa; độ dài trễ tối đa được chỉ định không chính xác có thể làm sai lệch hình dạng của cấu trúc độ trễ ước tính cũng như tác động tích lũy của biến độc lập. Độ trễ Almon giả định rằng k + 1 trọng số trễ có liên quan đến n + 1 tham số cơ bản có thể ước lượng tuyến tính ( n <k ) aj theo:
ωi= total(aj*ij)
Độ trễ phân phối vô hạn
Loại phổ biến nhất của mô hình trễ phân tán vô hạn có cấu trúc là độ trễ hình học , còn được gọi là độ trễ Koyck . Trong cấu trúc độ trễ này, trọng số (mức độ ảnh hưởng) của các giá trị biến độc lập bị tụt hậu giảm theo cấp số nhân với độ dài của độ trễ; trong khi hình dạng của cấu trúc trễ như vậy hoàn toàn được áp đặt bởi sự lựa chọn của kỹ thuật này, tốc độ suy giảm cũng như mức độ ảnh hưởng tổng thể được xác định bởi dữ liệu.
Đặc tả của phương trình hồi quy rất đơn giản: một phương trình bao gồm dưới dạng phần giải thích (các biến bên phải trong hồi quy) giá trị trễ một chu kỳ của biến phụ thuộc và giá trị hiện tại của biến độc lập:
Yt = Yt-1 + Xt + ECM
Ước lượng ARDL trên EViews
Hồi quy ARDL có mặt trên nhiều phần mềm, trong hướng dẫn này chúng tôi vấn tiếp tục cho chạy ARDL trên EViews ( Mô hình này bạn nên cho chạy Stata + R + Microfit … cũng rất tốt); Trong hồi quy này chúng tôi sẽ không thực hiện lại những bước trùng lặp trong mô hình tự hồi quy VAR, các bạn cần đọc mô hình đó trước.
- Chọn biến cho mô hình
Open > As Equation
- Trong hộp thoại mới
Method: ARDL – Autoregressive Distributed Lag model
Để giá trị mặc định và bấm OK, ta được kết quả sau:
| Variable | Coefficient | Std. Error | t-Statistic | Prob.* |
| LNPTV(-1) | 0.649019 | 0.094167 | 6.892234 | 0.0000 |
| LNPTV(-2) | 0.140015 | 0.074997 | 1.866933 | 0.0678 |
| LNPTV(-3) | -0.154475 | 0.057287 | -2.696529 | 0.0095 |
| LNPBL | 0.409585 | 0.101552 | 4.033250 | 0.0002 |
| LNPBL(-1) | -0.514120 | 0.084070 | -6.115365 | 0.0000 |
| LNPXK | 0.555296 | 0.142016 | 3.910104 | 0.0003 |
| C | -0.928118 | 0.448069 | -2.071374 | 0.0435 |
| R-squared | 0.957691 | Mean dependent var | 9.699666 | |
| Adjusted R-squared | 0.952614 | S.D. dependent var | 0.188167 | |
| S.E. of regression | 0.040961 | Akaike info criterion | -3.437820 | |
| Sum squared resid | 0.083889 | Schwarz criterion | -3.186918 | |
| Log likelihood | 104.9779 | Hannan-Quinn criter. | -3.340311 | |
| F-statistic | 188.6318 | Durbin-Watson stat | 2.089517 | |
| Prob(F-statistic) | 0.000000 | |||
Kiểm định chất lượng của hồi quy ARDL
Lag được chọn
View > Model Selection Summary > Criteria Graph
Bạn chọn table cũng được, nhưng chọn Graph cho dễ nhìn
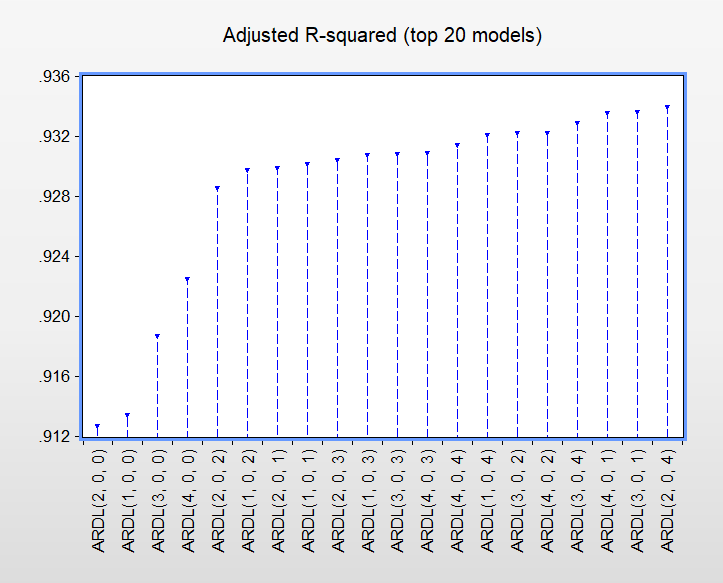
Phần mềm chọn ARDL(3,0,1)
Chúng ta chạy cho biết, vì chúng ta chọn chạy tự động ( Không giới hạn lag)..
Kiểm định phần phân phối chuẩn
Residuals Diagnostics > Histogram Normality test
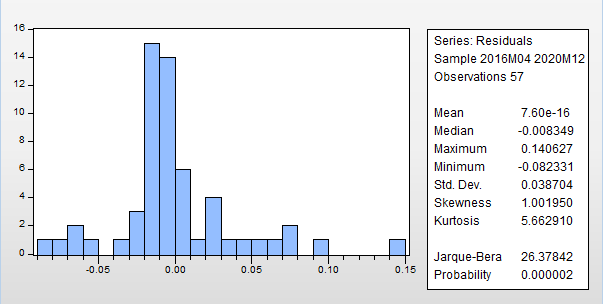
- Ta nhìn đồ thị nó không giống hình chuông và có nhiều khoảng trống, nên dữ liệu của chúng ta là chưa phân phối chuẩn.
- Kiểm định Jarque-Bera có P-value < 0.05 = > Dữ liệu chưa có phân phối chuẩn
Từ 2 nhận xét trên, chúng ta khẳng định dữ liệu không có phân phối chuẩn.
Kiểm định tương quan chuỗi
Residuals Diagnostics > Serial Correlations LM test
| Breusch-Godfrey Serial Correlation LM Test: | ||||
| F-statistic | 0.261190 | Prob. F(1,49) | 0.6116 | |
| Obs*R-squared | 0.302222 | Prob. Chi-Square(1) | 0.5825 | |
Ta có, P-Value > 0.05 = > Dữ liệu không bị tương quan chuỗi.
Kiểm định phương sai thay đổi
Eviews cho chúng ta rất nhiều kiểm định, chúng ta lựa chọn nhữ.ng kiểm định nào có lợi cho chúng ta thì chúng ta lấy.
Residuals Diagnostics > Heteroskedasticity Test
| Heteroskedasticity Test: Breusch-Pagan-Godfrey | ||||
| F-statistic | 3.263396 | Prob. F(6,50) | 0.0087 | |
| Obs*R-squared | 16.04017 | Prob. Chi-Square(6) | 0.0135 | |
| Scaled explained SS | 28.77573 | Prob. Chi-Square(6) | 0.0001 | |
Ta có P-value < 0.05 => Mô hình bị phương sai sai số thay đổi
Kiểm tra tính ổn định mô hình
Stability Diagnostic > Recusrive > CUMSUM
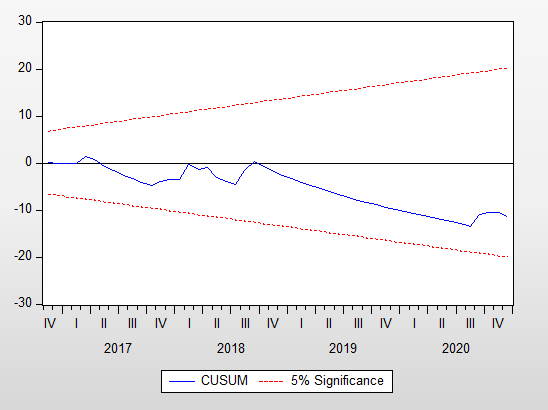
Ta có đường màu xanh luôn nằm trong giới hạn màu đỏ, chứng tỏ mô hình ổn định
Stability Diagnostic > Recusrive > CUMSUM of Square
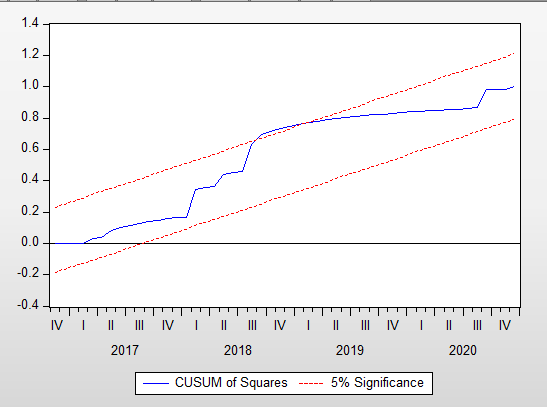
Ta thấy đường màu xanh đã vượt qua, ranh giới màu đỏ, chứng tỏ mô hình không ổn định.
Phân tích hồi quy ARDL
Giả sử các kiểm định trên phân bị sai phạm, chúng ta bắt đầu phân tích mô hình ARDL
Kiểm tra đồng liên kết
View > Coefficient Diagnostic > Long run & Bount test
| F-Bounds Test | Null Hypothesis: No levels relationship | |||
| Test Statistic | Value | Signif. | I(0) | I(1) |
| Asymptotic: n=1000 | ||||
| F-statistic | 6.396930 | 10% | 2.63 | 3.35 |
| k | 2 | 5% | 3.1 | 3.87 |
| 2.5% | 3.55 | 4.38 | ||
| 1% | 4.13 | 5 | ||
| Actual Sample Size | 57 | Finite Sample: n=60 | ||
| 10% | 2.738 | 3.465 | ||
| 5% | 3.288 | 4.07 | ||
| 1% | 4.558 | 5.59 | ||
| Finite Sample: n=55 | ||||
| 10% | 2.748 | 3.495 | ||
| 5% | 3.303 | 4.1 | ||
| 1% | 4.61 | 5.563 | ||
Ta có I(1) < Vaue = > Có mối quan hệ đồng liên kết.
Ước lượng Longrun
| Levels Equation | ||||
| Case 2: Restricted Constant and No Trend | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| LNPBL | -0.286053 | 0.329569 | -0.867959 | 0.3896 |
| LNPXK | 1.519522 | 0.433152 | 3.508059 | 0.0010 |
| C | -2.539721 | 1.353630 | -1.876229 | 0.0665 |
| EC = LNPTV – (-0.2861*LNPBL + 1.5195*LNPXK -2.5397 ) | ||||
Ước lượng ECM
| ECM Regression | ||||
| Case 2: Restricted Constant and No Trend | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| D(LNPTV(-1)) | 0.014460 | 0.058330 | 0.247905 | 0.8052 |
| D(LNPTV(-2)) | 0.154475 | 0.054702 | 2.823963 | 0.0068 |
| D(LNPBL) | 0.409585 | 0.079947 | 5.123172 | 0.0000 |
| CointEq(-1)* | -0.365441 | 0.070170 | -5.207973 | 0.0000 |
| R-squared | 0.819904 | Mean dependent var | 0.004831 | |
| Adjusted R-squared | 0.809710 | S.D. dependent var | 0.091202 | |
| S.E. of regression | 0.039785 | Akaike info criterion | -3.543083 | |
| Sum squared resid | 0.083889 | Schwarz criterion | -3.399711 | |
| Log likelihood | 104.9779 | Hannan-Quinn criter. | -3.487363 | |
| Durbin-Watson stat | 2.089517 | |||
Kết luận Mô hình tự phân phối độ trễ
- Đây là một mô hình rất hay dùng để dự báo trong kinh tế
- Phần lớn thì chúng ta chỉ quan tâm nhiều đến VAR/VECM
Giới thiệu dịch vụ
Nếu trong quá trình nghiên cứu khoa học định lượng, mà các bạn chạy model ARDL gặp những vấn đề sau:
- Sai phạm trong kiểm định
- Chưa biết đọc hiểu output
- Không biết cách áp dụng
- Chưa có data để chạy
- …
Nếu gặp những vấn đề trên, các bạn hãy liên hệ ngay với chúng tôi.




















0 nhận xét:
Đăng nhận xét