Xử lý biến trung gian mediator bằng macro PROCESS trong SPSS

 Một biến được gọi là biến trung gian khi nó tham gia giải thích cho mối quan hệ giữa biến độc lập và phụ thuộc (Baron & Kenny, 1986). Xem thêm thông tin ba loại biến biến trung gian, điều tiết, kiểm soát tại bài viết này.

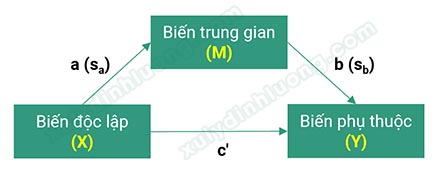
Mô hình biến trung gian cơ bản nhất gồm các biến và các mối tác động như sau:

Trong đó:

• c': Tác động trực tiếp direct effect từ X lên Y
• a*b: Tác động gián tiếp indirect effect từ X lên Y
• c: Tác động tổng hợp total effects từ X lên Y

Có những kỹ thuật xử lý biến trung gian khác nhau theo công trình nghiên cứu của các tác giả khác nhau. Dưới đây là hai kỹ thuật được sử dụng phổ biến cho tới hiện tại. Mỗi kỹ thuật có cách thức tiếp cận khái niệm biến trung gian và cơ chế xác định mối quan hệ trung gian khác nhau. 

1. Xử lý biến trung gian mediator bằng Sobel Test

Theo Baron & Kenny (1986), một biến được xác định là đóng vai trò trung gian nếu thỏa mãn cùng lúc 3 điều kiện sau đây:

1. Điều kiện 1: Biến độc lập có tác động lên biến trung gian (a ≠ 0).
2. Điều kiện 2: Biến trung gian có tác động lên biến phụ thuộc (b ≠ 0).
3. Điều kiện 3: Khi điều kiện 1 và 2 thỏa mãn, sự xuất hiện của biến trung gian sẽ làm giảm sự tác động từ biến độc lập lên biến phụ thuộc (c' < c), trong đó c là hệ số hồi quy từ X lên Y khi chưa có sự hiện diện của biến trung gian M.

Để kiểm tra một biến trung gian có thỏa được 3 điều kiện ở trên hay không, chúng ta sẽ thực hiện 3 phép hồi quy như sau:

1. Hồi quy đơn: X → M: Để biết biến độc lập có tác động lên biến trung gian hay không (điều kiện 1). Kết quả mong đợi là sig kiểm định t của biến X nhỏ hơn 0.05.

M = hằng số 1 + aX + e1

2. Hồi quy bội: X, M → Y: Để biết biến trung gian có tác động lên biến phụ thuộc hay không (điều kiện 2). Kết quả mong đợi là sig kiểm định t của biến M nhỏ hơn 0.05.

Y = hằng số 2 + c'X + bM + e2

3. Hồi quy đơn: X → Y: Để biết sự xuất hiện của biến trung gian có làm giảm sự tác động từ biến độc lập lên biến phụ thuộc hay không. Kết quả mong đợi là hệ số c' < c.

Y = hằng số 3 + cX + e3

Nếu 1 trong 3 điều kiện trên bị vi phạm, biến M không đóng vai trò trung gian can thiệp vào sự tác động từ X lên Y.

Trên cơ sở lý thuyết ở trên, chúng ta sẽ đi vào thực hiện đánh giá quan hệ trung gian bằng Sobel Test (Sobel, 1982) trên SPSS bằng cách giải quyết lần lượt từng hồi quy. Các bạn có thể tải tập dữ liệu thực hành tại đây, sau khi tải về các bạn giải nén để mở tệp tin Mediation File.sav thực hành. 

Tập dữ liệu này sẽ gồm 3 biến X, M, Y tương ứng biến độc lập, trung gian, phụ thuộc. Biến độc lập là chất lượng dịch vụ, biến trung gian là sự hài lòng và biến phụ thuộc là ý định quay lại. Cả 3 biến đều được đánh giá bằng thang đo Likert 5 mức độ. Thực hiện phân tích biến trung gian bằng Sobel Test để xem Sự hài lòng có vai trò trung gian tác động lên mối quan hệ giữa Chất lượng dịch vụ với Ý định quay lại của khách hàng hay không.

Bước 1: Thực hiện hồi quy đơn X → M

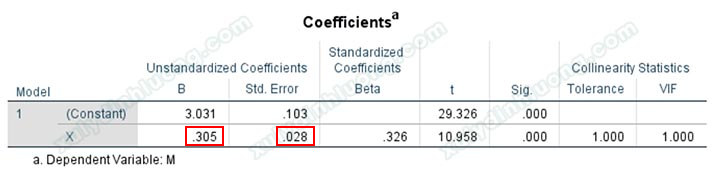
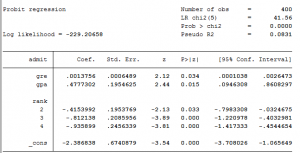
Xem cách thực hiện hồi quy trên SPSS tại bài viết này. Chúng ta có sig kiểm định t của biến X bằng 0.000 < 0.05, biến X có tác động lên M. Hệ số tác động chưa chuẩn hóa và sai số chuẩn của X lần lượt: a = 0.305 và sa = 0.026 (các ký hiệu a, sa chúng ta sẽ dùng ở Sobel Test).

Bước 2: Thực hiện hồi quy bội X, M → Y

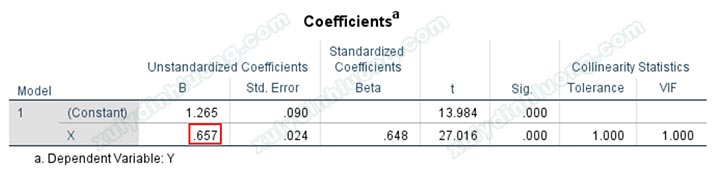
Chúng ta có sig kiểm định t của biến M bằng 0.000 < 0.05, biến M có tác động lên Y. Hệ số tác động chưa chuẩn hóa và sai số chuẩn của M lần lượt: b = 0.104 và sb = 0.027. Hệ số tác động chưa chuẩn hóa của X trong phép hồi quy này là c' = 0.626.

Bước 3: Thực hiện hồi quy đơn X → Y

Chúng ta có hệ số tác động chưa chuẩn hóa c = 0.657 > c' = 0.626, điều này cho thấy biến trung gian M đã làm giảm tác động của biến độc lập lên biến phụ thuộc. Tại đây, theo lý thuyết của Barron (1986) chúng ta sẽ kết luận biến M đóng vai trò trung gian tác động lên mối quan hệ của X và Y.

Hiệu số c - c' = 0.657 - 0.626 = 0.031 (cũng chính bằng tích số a*b) cho chúng ta thấy có sự khác biệt. Tuy nhiên, sự khác biệt này có ý nghĩa thống kê hay không, c lớn hơn c' có ý nghĩa thống kê hay không, chúng ta cần phải thực hiện kiểm định t để đánh giá. Phép kiểm định t đánh giá hiệu số c - c' có nghĩa thống kê hay không được gọi là Sobel Test (xem thêm tại đây). Do đó, chúng ta sẽ tiếp tục thực hiện bước 4.

Bước 4: Đánh giá sự khác biệt c - c'  bằng Sobel Test.

SPSS không tích hợp sẵn Sobel Test, chúng ta sẽ thực hiện kiểm định tại website này. Sau khi truy cập vào website, chúng ta sẽ chú ý tới phần Input với 4 giá trị cần khai báo đầu vào là a, b, sa, sb. Với:

• a, sa: lần lượt là hệ số hồi quy chưa chuẩn hóa và sai số chuẩn của X trong phương trình hồi quy đơn X → M.
• b, sb: lần lượt là hệ số hồi quy chưa chuẩn hóa và sai số chuẩn của M trong phương trình hồi quy bội X, M → Y.

Nhập 4 giá trị a, b, sa, sb tương ứng vào các ô trên bảng Sobel Test, sau đó nhấn vào Calculate để tiến hành phân tích. Chúng ta sẽ đọc kết quả giá trị p-value ở phần bôi vàng.

Giá trị sig (p-value) của kiểm định Sobel bằng 0.000 < 0.05, như vậy M là biến trung gian tác động lên mối quan hệ từ X lên Y.

2. Xử lý biến trung gian mediator bằng Bootstrap với macro PROCESS

Với lý thuyết của Baron & Kenny (1986) về biến trung gian và mối tác động trung gian, một điều kiện cần đó là biến độc lập X phải có sự tác động lên biến phụ thuộc Y (tác động tổng hợp total effect - hệ số c phải có ý nghĩa). 

Trong đó:

• c': Tác động trực tiếp direct effect từ X lên Y
• a*b: Tác động gián tiếp indirect effect từ X lên Y
• c: Tác động tổng hợp total effects từ X lên Y

Tuy nhiên, một số tác giả (Collins, Graham, & Flaherty, 1998; Judd & Kenny, 1981; Kenny et al., 1998; MacKinnon, 1994, 2000; MacKinnon, Krull, & Lockwood, 2000; Shrout & Bolger, 2002) đã đưa ra tranh cãi rằng, mối tác động tổng hợp total effects không nhất thiết phải có ý nghĩa thì mới có mối quan hệ trung gian. Do đó, chúng ta cần có một hướng đánh giá mối quan hệ trung gian chính xác hơn.

Bootstrapping là một kỹ thuật liên quan đến việc lấy mẫu lặp lại từ tập dữ liệu mẫu và ước tính tác động gián tiếp indirect (tích số a*b) trong mỗi tập dữ liệu được lấy mẫu lại. Bằng cách lặp lại quá trình này, phân phối của tích số a*b được hình thành và tạo nên khoảng tin cậy (Confidence Interval) của mối quan hệ gián tiếp indirect effects (Preacher and Hayes, 2004).

Nhiều nghiên cứu đã chứng minh kỹ thuật Bootstrapping tốt hơn Sobel Test và các kỹ thuật khác khi đánh giá mối quan hệ trung gian (Williams & MacKinnon, 2008; Preacher & Hayes, 2008; Zhao, Lynch & Chen, 2010). Trong khi Sobel Test yêu cầu cỡ mẫu lớn và dữ liệu cần có phân phối chuẩn thì Bootstrapping khắc phục được các hạn chế này (Hayes, 2009). Chính vì vậy mà hiện nay, kỹ thuật xử lý biến trung gian bằng Bootstrap được sử dụng phổ biến hơn so với Sobel Test.

ư

 Xem thêm: Xử lý biến điều tiết moderator trong SPSS

Để thực hiện phân tích biến trung gian bằng Bootstrap trên SPSS, chúng ta sẽ dụng Hayes Process Macro. Các bạn tải Macro này tại https://www.processmacro.org/download.html, cách tải và cài đặt vào SPSS, các bạn xem ở video bên dưới.

Mở tệp dữ liệu SPSS cần chạy phân tích trung gian, vào Analyze > Regression > PROCESS v3.5 by Andrew F. Hayes (macro cập nhật liên tục theo thời gian, do vậy số phiên bản 3.5 có thể thay đổi).

Cửa sổ PROCESS xuất hiện, chúng ta đưa biến phụ thuộc vào Y variable, biến độc lập vào X variable, biến trung gian vào Mediator(s). Nếu có nhiều biến trung gian cùng tác động lên mối quan hệ X, Y, chúng ta có thể đưa tất cả vào cùng lúc. Chọn các tùy chọn giống như mục số 2, sau đó nhấp vào Options mục 3.

Trong Options, tích vào 2 lựa chọn ở mục 1 và thiết lập mục 2 như ảnh. Nhấp Continue để quay lại cửa sổ ban đầu, sau đó nhấp OK để xuất kết quả ra Output. 

Tương tự như Sobel Test, Macro PROCESS cũng xuất kết quả các phép hồi quy X → M (hồi quy 1) và X, M → Y (hồi quy 2). Bởi vì mỗi lần chạy Bootstrap, phần mềm sẽ lấy mẫu khác nhau nên kết quả có sự sai biệt giữa ảnh bên dưới với phần thực hành là bình thường, không phải lỗi.

(Kết quả phép hồi quy từ X lên M)

(Kết quả phép hồi quy từ X, M lên Y)

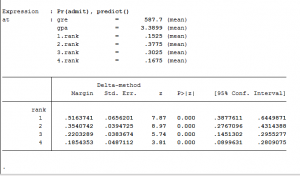
Chúng ta quan tâm nhiều nhất vào mối quan hệ gián tiếp của X lên Y. Do vậy, cần tập trung vào bảng TOTAL, DIRECT AND INDIRECT EFFECTS OF X ON Y.

• Total effect of X on Y: Tổng tác động từ X lên Y (hệ số c)
• Direct effect of X on Y: Tác động trực tiếp từ X lên Y (hệ số c')
• Indirect effect(s) of X on Y: Tác động gián tiếp từ X lên Y qua M (tích số a*b)

Phần Indirect effects chúng ta sẽ đánh giá có sự tác động gián tiếp hay không dựa vào khoảng tin cậy phép bootstrap cho tích số a*b .

• Nếu khoảng tin cậy phép bootstrap tích số a*b chứa giá trị 0, chúng ta kết luận không có tác động gián tiếp từ X lên Y.
• Nếu khoảng tin cậy phép bootstrap tích số a*b không chứa giá trị 0, chúng ta kết luận có tác động gián tiếp từ X lên Y.

Cụ thể trong ví dụ thực hành, từ đầu chúng ta chọn độ tin cậy là 95%, kết quả cho gá trị dưới BootLLCI (Lower-Level Confidence Interval) bằng 0.0139 và giá trị trên BootULCI (Upper-Level Confidence Interval) bằng 0.0509. Khoảng tin cậy [0.0139; 0.0509] không bao gồm giá trị 0, như vậy có tác động gián tiếp từ X lên Y qua M với mức tác động là 0.0317. Như vậy, biến M có vai trò trung gian tác động lên mối quan hệ từ X tới Y.

Read More

Hệ số tương quan biến tổng Corrected Item – Total Correlation là gì?

 Hệ số tương quan biến tổng (Corrected Item – Total Correlation) có ý nghĩa quan trọng trong phân tích độ tin cậy thang đo Cronbach’s Alpha, giúp nhà nghiên cứu xác định được biến quan sát nào ít đóng góp cho thang đo và từ đó, cân nhắc việc loại bỏ biến quan sát để tăng độ tin cậy cho thang đo.

Trong 2 tiêu chuẩn để đánh giá về độ tin cậy thang đo Cronbach’s Alpha đã được đề cập trong bài viết Phân tích độ tin cậy Cronbach’s Alpha trong SPSS, chỉ số tương quan biến tổng Corrected Item – Total Correlation nếu nhỏ hơn 0.3, thì biến quan sát cần được loại bỏ. Vậy ý nghĩa của hệ số này là gì và tại sao khi nó nhỏ hơn 0.3 thì cần được loại bỏ?

Tương quan biến tổng Corrected Item – Total Correlation là chỉ số của từng biến quan sát chứ không phải là chỉ số của cả 1 thang đo. Khi trình bày trong bảng kết quả Item-Total Statistics, chỉ số này sẽ hiện ở từng hàng tương ứng với từng biến quan sát DK1 – DK4 ở ví dụ bên trên.

Một thang đo có độ tin cậy cao (hệ số Cronbach Alpha cao) khi các biến quan sát của nó có sự tương quan chặt chẽ với nhau. Sự tương quan này càng lớn cho thấy rằng các biến quan sát biểu hiện rất tốt cho đặc điểm, tính chất của biến mẹ, trừ một số trường hợp vi phạm trùng lặp thang đo.

Corrected Item – Total Correlation thể hiện mối quan hệ giữa biến quan sát đó với tất cả các biến quan sát còn lại trong cùng 1 thang đo (cùng 1 nhóm). Chỉ số này càng cao, nghĩa là biến quan sát tương quan càng mạnh với các biến còn lại, biến này càng tốt và ngược lại, chỉ số này càng thấp, tương quan với các biến còn lại càng thấp, biến này càng không tốt.

Nhà nghiên cứu luôn kỳ vọng các thang đo của mình đều đạt được Cronbach’s Alpha cao để nghiên cứu có độ tin cậy cao. Điều này đồng nghĩa, các biến quan sát của một thang đo cần phải tương quan chặt chẽ với nhau. Trường hợp có biến quan sát tương quan yếu với các biến còn lại, Corrected Item – Total Correlation thấp, biến đó cần được loại bỏ. Vậy thì mức thấp là bao nhiêu thì nên loại biến quan sát đó? Dưới đây là một số ngưỡng được đề xuất bởi các nhà nghiên cứu:

• 0.30 by Nunnally, J. C., & Bernstein, I. H. (1994)
• 0.30 by Cristobal et al. (2007)
• 0.40 by Loiacono et al. (2002)
• 0.50 by Francis and White (2002) and Kim and Stoel (2004)

Trong các ngưỡng này mức 0.3 được sử dụng phổ biến nhất hiện nay. Việc chọn các ngưỡng 0.4 hay 0.5 là những mức cao hơn, giúp cho nhà nghiên cứu chọn lọc ra những biến quan sát tốt nhất của thang đo. Từ đây, chúng ta có thể hình dung được, khi chúng ta có rất nhiều biến quan sát cho một thang đo, tầm trên 7 quan sát thì có thể chúng ta cân nhắc việc chọn ngưỡng 0.4 hoặc 0.5 để chọn ra được các biến quan sát tốt nhất. Nếu thang đo của bạn ít biến quan sát thì nên chọn mức 0.3 để giữ lại nhiều biến quan sát nhất có thể và các biến quan sát này cũng phản ánh ở mức khá đặc điểm của nhân tố mẹ.

Read More

Tạo nhân tố, biến đại diện sau phân tích EFA

Kết thúc bước EFA, chúng ta sẽ tiến hành tạo nhân tố đại diện (biến đại diện) phục vụ cho bước phân tích tương quan quan, hồi quy, phương sai…

Mục đích cuối cùng của phần phân tích định lượng là trả lời cho các giả thuyết đặt ra: các biến độc lập có sự tác động lên biến phụ thuộc hay không. Bởi vì các biến độc lập và phụ thuộc là các khái niệm trừu tượng, chúng ta mới xây dựng các thang đo biến quan sát để làm công cụ đo lường trung gian. Tuy nhiên, không phải lúc nào các biến quan sát cho mỗi nhân tố chúng ta xây dựng đều có ý nghĩa trong thang đo, chúng ta cần thực hiện kiểm định độ tin cậy Cronbach’s Alpha và phân tích nhân tố EFA để chọn lọc giữ lại các biến quan sát tốt và loại bỏ các biến quan sát kém chất lượng. Kết thúc bước chọn lọc, chúng ta có được các nhân tố phù hợp nhất với các biến quan sát tốt nhất. Lúc này, chúng ta sẽ cần chuyển hướng việc đo lường biến quan sát về đo lường nhân tố để kết luận được các giả thuyết đặt ra, bước chuyển đổi này được gọi là tạo nhân tố đại diện.

Sau EFA, chúng ta có được các nhân tố giống hoặc không giống với cấu trúc nhân tố lý thuyết. Chúng ta thực hiện tạo nhân tố đại diện dựa trên kết quả ma trận xoay EFA cuối cùng. Bên dưới là bảng tổng hợp các nhân tố sau phân tích EFA và ký hiệu mã hóa nhân tố đại diện:

 

Khi đặt ký hiệu cho nhân tố đại diện (biến đại diện), chúng ta nên thêm tiền tố “F_” trước ký hiệu để tránh trùng ký tự đặc biệt trong SPSS trong một số trường hợp. Nếu tên biến được khai báo vi phạm nguyên tắc của SPSS, một bảng thông báo “Name contain a reserved word” sẽ xuất hiện.

Có ba cách tạo biến đại diện được sử dụng hiện nay, chúng ta sẽ lần lượt đi qua từng cách với ví dụ minh họa.

1. Tạo nhân tố đại diện bằng trung bình cộng

Biến đại diện được tạo bằng cách tính trung bình cộng các biến quan sát của nhân tố đó. Với các nghiên cứu sử dụng thước đo Likert, hay các thước đo ảo với giá trị đo là số nguyên thì cách xây dựng biến đại diện bằng cách này rất phù hợp. Nó sẽ giúp ích cho nhà nghiên cứu có thể triển khai các bước phân tích sau hồi quy mà không gặp nhiều khó khăn. Từ bảng tổng hợp các nhân tố sau phân tích EFA, trên giao diện SPSS, chúng ta vào Transform > Compute Variables…

Một cửa sổ mới được mở ra, chúng ta chú ý tới 2 mục là Target Variable bên trái và khung nhập hàm Numeric Expression bên phải:

• Target Variable: Điền tên biến đại diện. Cụ thể ở đây là nhân tố F_TL.
• Numeric Expression: Nhập hàm MEAN(giá trị 1,giá trị 2,giá trị 3,…). Cụ thể ở đây là MEAN(TL1,TL2,TL3,TL4). Tên hàm có thể viết hoa hoặc viết thường, các giá trị trong hàm ngăn cách nhau bằng dấu phẩy và không có khoảng cách trắng.

Khi khai báo tên biến, chúng ta có thể vào Type & Label để nhập nhãn biến. Phần này không bắt buộc, có thể điền hoặc không điền.

Sau khi khai báo biến, hàm, nhãn biến, nhấp vào OK để xác nhận hoàn thành. Lúc này quay lại giao diện Variable View của SPSS, sẽ có một biến mới được tạo ra tên là F_TL. Thực hiện tương tự cho các biến còn lại, chúng ta sẽ có danh sách biến đại diện như bên dưới.

Sau khi đã hoàn thành việc tạo biến đại diện, chúng ta nên quay lại giao diện Variable View, chỉnh Decimals cho các biến đại diện là 2. Biến đại diện là trung bình của nhiều biến quan sát nên thường kết quả sẽ trả về số thập phân, nếu chúng ta để Decimals về 0 sẽ không hợp lý lắm vì ta đã làm tròn về dạng số nguyên. Do vậy, chúng ta nên làm tròn 2 chữ số thập phân, nhìn vào kết quả sẽ hợp lý và tự nhiên hơn.

Ưu điểm: dễ hiểu, có thể ứng dụng nhân tố đại diện cho nhiều phân tích khác, đặc biệt là phân tích khác biệt trung bình sẽ được giới thiệu ở chương 13.

Nhược điểm: không xét đến vai trò đóng góp của các biến quan sát trong nhóm, tầm quan trọng các biến quan sát đều được đánh đồng như nhau.

2. Tạo nhân tố đại diện bằng tổng giá trị

Thay vì tính trung bình cộng giá trị các biến quan sát thuộc nhân tố, chúng ta cũng có thể tạo biến đại diện bằng tổng giá trị các biến quan sát đó. Cách thực hiện tương tự như tạo nhân tố đại diện bằng trung bình cộng, chúng ta vào Transform > Compute Variables… Lần lượt nhập tên biến vào Target Variable, nhập nhãn biến vào Type & Label, và nhập hàm tính vào Numeric Expression. Lúc này, thay vì nhập hàm trung bình cộng MEAN, chúng ta sẽ sử dụng hàm tổng SUM theo cấu trúc SUM(giá trị 1,giá trị 2,giá trị 3,…). Cụ thể ở đây là SUM(TL1,TL2,TL3,TL4). Tên hàm có thể viết hoa hoặc viết thường, các giá trị trong hàm ngăn cách nhau bằng dấu phẩy và không có khoảng cách trắng.

Với cách tạo biến đại diện này, hầu hết các phân tích về sau đều cho ra kết quả giống với cách tính từ trung bình cộng. Do vậy, nhà nghiên cứu chỉ cần chọn một trong hai cách để sử dụng.

Ưu điểm: dễ hiểu, có thể ứng dụng nhân tố đại diện cho nhiều phân tích khác.

Nhược điểm: không xét đến vai trò đóng góp của các biến quan sát trong nhóm, tầm quan trọng các biến quan sát đều được đánh đồng như nhau.

3. Tạo nhân tố đại diện bằng điểm nhân tố

Phương thức này mang nhiều khác biệt so với hai cách ở trên. Nếu dùng trung bình cộng và tổng, sự đóng góp các biến quan sát trong nhân tố không được xét đến thì với cách thứ ba này, nhân tố đại diện phản ánh chính xác nhất đặc điểm của các biến quan sát. Những biến quan sát có hệ số tải cao, nghĩa là có đóng góp nhiều vào nhân tố sẽ được tính điểm nhiều hơn vào biến đại diện. Để thực hiện tạo nhân tố đại diện bằng điểm nhân tố, tại giao diện Factor Analysis, chúng ta vào Scores…, sau đó tích vào mục Save as variables.

Lưu ý, với phương thức này, chúng ta chỉ thực hiện bước tạo biến đại diện sau lần phân tích EFA cuối cùng, bởi mỗi lần chúng ta thực hiện EFA, biến đại diện lại được tạo ra. Nếu bạn cần loại nhiều biến xấu cần phân tích nhiều lần EFA, mỗi lần như vậy SPSS sẽ tạo ra các biến đại diện dựa vào kết quả ma trận xoay. Số biến đại diện không hoàn chỉnh sẽ tạo ra liên tục đến khi bạn ngưng phân tích EFA, lúc này trong khuôn dữ liệu của bạn sẽ có rất nhiều biến đại diện không dùng đến. Việc này không ảnh hưởng đến kết quả phân tích, tuy nhiên về mặt thẩm mỹ và tính trực quan, chúng ta không nên để xuất hiện quá nhiều biến thừa trong dữ liệu.

Ưu điểm: nhân tố đại diện được xây dựng dựa trên mức độ đóng góp của các biến quan sát, nhờ vậy, nhân tố biểu thị tốt đặc điểm của các biến quan sát hơn.

Nhược điểm: biến đại diện được tạo chỉ sử dụng vào phân tích hồi quy tuyến tính; ngoài ra, các biến đại diện đều đã được chuẩn hóa nên chúng ta không đánh giá được một số giả định trong hồi quy quan trọng.

Read More

Dịch vụ xử lý dữ liệu của Xử Lý dữ liệu nghiên cứu Định Lượng

 Dưới đây là thông tin chi tiết về Quy trình và Thanh toán khi sử dụng dịch vụ xử lý dữ liệu của Xử Lý Định Lượng:

Bước 1: Gửi thông tin xử lý qua email

Bạn gặp khó khăn khi phân tích dữ liệu và muốn sử dụng các gói dịch vụ STATA, EVIEWS, SPSS, AMOS, SMARTPLS, để liên hệ nhanh nhất bạn vui lòng nhắn tin qua zalo  gửi email tới nckhdinhluong@gmail.com, đính kèm các tập tin liên quan và mô tả vấn đề cần Xử Lý Định Lượng hỗ trợ.

Bước 2: Hoàn chỉnh thông tin xử lý

Xử Lý Định Lượng tiếp nhận thông tin, tư vấn thêm để bạn hoàn thiện những chỗ còn thiếu sót và đưa ra hướng giải quyết vấn đề bạn đang gặp.

Bước 3: Xác nhận thông tin và báo chi phí, thời gian xử lý

Sau khi trao đổi và thống nhất mọi thông tin, Xử Lý Định Lượng báo chi phí và thời gian xử lý dữ liệu.

Bước 4: Đặt cọc phí xử lý

Bạn sẽ chuyển khoản đặt cọc chi phí (thường là 70% chi phí gói xử lý) để xác nhận chắc chắn bạn sẽ nhận dữ liệu sau khi xử lý.

Bước 5: Gửi kết quả xử lý

Xử Lý Định Lượng xử lý dữ liệu và gởi kết quả xử lý cho bạn bằng file PDF. Bạn có thời gian  5 ngày (tính từ ngày gửi file PDF) để xem kết quả và phản hồi về việc điều chỉnh lại kết quả hoặc hoàn tất phí để nhận kết quả xử lý. Sau 5 ngày này, nếu không có bất kỳ phản hồi nào từ phía bạn, Xử Lý Định Lượng mặc định bạn không nhận kết quả, team sẽ hủy toàn bộ dữ liệu và kết quả đã xử lý.

Bước 6: Gửi dữ liệu, hoàn tất dịch vụ

Bạn đồng ý kết quả xử lý và muốn nhận dữ liệu, các file kết quả liên quan. Bạn vui lòng hoàn tất phí và báo với Xử Lý Định Lượng qua zalo  gửi email tới nckhdinhluong@gmail.com. Các file bạn sẽ nhận được sau khi hoàn tất phí:

Với dịch vụ STATA

– File dữ liệu đã xử lý hoàn chỉnh dạng DTA, SCML + dạng Excel.

– File word kết quả xuất các bảng cần thiết trong các kiểm định + diễn giải cơ bản các chỉ số

Với dịch vụ SPSS:

– File dữ liệu đã xử lý hoàn chỉnh dạng SPSS + dạng Excel.

– File word kết quả xuất các bảng cần thiết trong các kiểm định + diễn giải cơ bản các chỉ số.

Với dịch vụ AMOS:

– File dữ liệu đã xử lý hoàn chỉnh dạng SPSS + dạng Excel.

– File diagram CFA + SEM của AMOS.

– File word kết quả xuất các bảng cần thiết trong các kiểm định + diễn giải cơ bản các chỉ số.

Với dịch vụ SMARTPLS:

– File dữ liệu đã xử lý hoàn chỉnh dạng Excel.

– File project của SMARTPLS.

– File word kết quả xuất các bảng cần thiết trong các kiểm định + diễn giải cơ bản các chỉ số.

Read More

Hướng Dẫn Hồi Quy Mô Hình Probit Trên Stata

 

Tìm hiểu về mô hình probit

Hồi quy probit, còn được gọi là mô hình probit, được sử dụng để mô hình các biến kết cục nhị phân hoặc nhị phân. Trong mô hình probit, phân phối chuẩn của nghịch đảo xác suất được mô hình hóa như một tổ hợp tuyến tính của các yếu tố dự đoán.

Xin lưu ý: Mục đích của trang này là hiển thị cách sử dụng các lệnh phân tích dữ liệu khác nhau. Nó không bao gồm tất cả các khía cạnh của quá trình nghiên cứu mà các nhà nghiên cứu dự kiến ​​sẽ làm. Đặc biệt, nó không bao gồm việc làm sạch và kiểm tra dữ liệu, xác minh các giả định, chẩn đoán mô hình và phân tích theo dõi tiềm năng.

Một mô hình probit là một đặc điểm kỹ thuật phổ biến cho một mô hình phản ứng nhị phân  hoặc nhị phân . Do đó, nó xử lý cùng một tập hợp các vấn đề như hồi quy logistic bằng các kỹ thuật tương tự. Mô hình probit, sử dụng hàm liên kết probit , thường được ước tính bằng cách sử dụng thủ tục khả năng tối đa tiêu chuẩn , một ước tính như vậy được gọi là hồi quy probit .

Ứng dụng hồi quy mô hình probit

Để bắt đầu tìm hiểu về hồi quy mô hình probit ta sử dụng bộ dữ liệu sau:

 

Trong đó:

• admint: biết nhị phân cũng là biến phụ thuộc
• gre, gpa là biến liên tục
• rank là biến thứ bậc

Đọc thêm:   Ứng dụng mạng nơron trong dự báo ARIMA

Trước khi hồi quy chúng ta cần xem lại một số kiến thức như sau:

Dưới đây là danh sách một số phương pháp phân tích mà bạn có thể đã gặp phải. Một số phương pháp được liệt kê là khá hợp lý trong khi các phương pháp khác không được ưa chuộng hoặc có những hạn chế.

Hồi quy probit, trọng tâm của bài này

Hồi quy logistic. Một mô hình logit sẽ tạo ra kết quả tương tự hồi quy probit. Sự lựa chọn của probit so với logit phụ thuộc phần lớn vào sở thích cá nhân.

Hồi quy OLS. Khi được sử dụng với biến phản ứng nhị phân, mô hình này được biết đến như một mô hình xác suất tuyến tính và có thể được sử dụng như một cách để mô tả xác suất có điều kiện. Tuy nhiên, các lỗi (nghĩa là phần dư) từ mô hình xác suất tuyến tính vi phạm tính đồng nhất và tính quy phạm của các giả định lỗi của OLS hồi quy, dẫn đến các lỗi tiêu chuẩn và kiểm tra giả thuyết không hợp lệ.

Dành cho một cuộc thảo luận kỹ lưỡng hơn về những vấn đề này và các vấn đề khác với tuyến tính mô hình xác suất, xem Long (1997, trang 38-40).

Phân tích chức năng phân biệt hai nhóm. Một phương pháp đa biến cho các biến kết cục nhị phân. Khách sạn T 2 . Kết quả 0/1 được chuyển thành nhóm biến, và các dự đoán trước đây được biến thành kết quả biến. Điều này sẽ tạo ra một bài kiểm tra tổng thể có ý nghĩa nhưng sẽ không đưa ra các hệ số riêng cho từng biến và không rõ phạm vi mà mỗi “yếu tố dự đoán” được điều chỉnh theo tác động của cái khác “dự đoán.”

Hồi quy probit

Để hồi quy probit ta sử dụng lệnh như sau:

probit admit gre gpa rank

Ta có P-Value <5%, nên mô hình có ý nghĩa thống kê.

Đồng thời 3 biến phụ thuộc là gre, gpa, rank điều có giá trị p-value <5%, nên 3 biến này điều có ý nghĩa thống kê.

Khi gre tăng 1 đơn vị thì z-score tăng 0.001 đơn vị

Khi gpa tăng 1 đơn vị thì z-core tăng 0.464 đơn vị

Còn biến rank là biến thư bậc, nên khi rank tăng lên 1 bậc thì điểm z sẽ giảm đi  -2,01. điều này có nghĩa là các bậc tăng hay giảm trong mô hình điều như nhau, điều này thật không đúng. Chúng ta cần phải tìm cho chính xách mức độ ảnh hưởng của rank =3 thì tác động lên admit như thế nào ?

probit admit gre gpa i.rank

Những đơn vi tham gia vào rank=2 so với những đơn vị tham gia vào rank=1, sẽ lam giảm đi 0.4 đơn vị điểm z.

Nhân tiện đây chúng ta kiểm định các biến phụ thuộc của rank không đồng thời bằng =0

test 2.rank 3.rank 4.rank

Kiểm định cho thấy các biến độc lập i.rank không phụ thuộc vào nhau, tác có tác động độc lập đến admit.

Tìm độ nhạy biên của mô hình

chúng ta tìm độ nhạy của biến xếp hạng rank lên biến admit

margin rank, atmean

Sau khi chúng ta chạy margin chúng  ta có kết quả như sau:

Chúng ta có xác suất tổ chức được xếp vào rank=1 là 0.52 (52%), xác suất được xếp vào rank=4 là 19%. 

Kiểm tra thống kê phù hợp fitstat

trong hồi quy mô hình probit chúng ta nên kiểm tra thống kê phù hợp. 

Những điều cần cân nhắc

Các ô trống hoặc ô nhỏ: Bạn nên kiểm tra trống hay nhỏ các tế bào bằng cách thực hiện một dấu chéo giữa các yếu tố dự đoán phân loại và biến kết quả. Nếu một ô có rất ít trường hợp (một ô nhỏ), mô hình có thể trở nên không ổn định hoặc nó có thể không chạy được gì cả.

Tách hoặc tách biệt (còn gọi là dự đoán hoàn hảo), một điều kiện trong đó kết quả không thay đổi ở một số cấp độ của các biến độc lập. Xem trang của chúng tôi Câu hỏi thường gặp: Sự tách biệt hoàn toàn hoặc gần như hoàn toàn trong hồi quy logistic / probit và làm thế nào để chúng ta đối phó với chúng? để biết thông tin về các mô hình với dự đoán hoàn hảo.

Cỡ mẫu: Cả hai mô hình probit và logit đều yêu cầu nhiều trường hợp hơn hồi quy OLS vì chúng sử dụng các kỹ thuật ước tính khả năng tối đa. Đôi khi có thể ước tính các mô hình cho kết quả nhị phân trong bộ dữ liệu chỉ với một số ít trường hợp sử dụng hồi quy logistic chính xác (sử dụng lệnh exlogistic ). Để biết thêm thông tin, xem ví dụ phân tích dữ liệu của chúng tôi để biết hồi quy logistic chính xác . Cũng cần lưu ý rằng khi kết quả rất hiếm, ngay cả khi tổng số liệu lớn, có thể khó ước tính mô hình probit.

Pseudo-R-squared: Nhiều biện pháp khác nhau của psuedo-R-squared tồn tại. Tất cả đều cố gắng cung cấp thông tin tương tự như thông tin được cung cấp bởi R bình phương trong hồi quy OLS; tuy nhiên, không ai trong số chúng có thể được hiểu chính xác như bình phương R trong hồi quy OLS được diễn giải. Để thảo luận về các giả bình phương R khác nhau, hãy xem Long và Freese (2006) hoặc trang Câu hỏi thường gặp của chúng tôi Giả R bình phương là gì? 

Trong Stata, các giá trị 0 được coi là một cấp của biến kết quả, và tất cả các giá trị không thiếu khác được coi là mức thứ hai của kết quả.

Chẩn đoán: Chẩn đoán hồi quy probit khác với chẩn đoán hồi quy OLS. Chẩn đoán cho các mô hình probit tương tự như các mô hình cho mô hình logit. Để thảo luận về chẩn đoán mô hình cho hồi quy logistic, xem Hosmer và Lemeshow (2000, Chương 5).

Read More