Ước lượng GMM là gì ?
GMM, viết tắt của Generalized Method of Moments, là tên chung của một họ phương pháp hồi quy/ước lượng (estimation) để xác định các thông số của mô hình thống kê hoặc mô hình kinh tế lượng. GMM được sử dụng để tìm/dự tính các thông số của mô hình parametric và non-parametric.
GMM được phát triển bởi Lars Peter Hansen năm 1982 từ việc tổng quát hóa phương pháp hồi quy theo moments.
GMM được sử dụng nhiều cho dự liệu mảng (panel data), đặc biệt khi T nhỏ hơn N nhiều lần, hoặc dữ liệu không đồng nhất.
Mục đích của ước lượng GMM
Trong kinh tế lượng và thống kê , phương pháp tổng quát của các khoảnh khắc ( GMM ) là một phương pháp chung để ước tính các tham số trong các mô hình thống kê . Thông thường, nó được áp dụng trong ngữ cảnh của các mô hình bán tổng thể , trong đó tham số quan tâm là chiều hữu hạn, trong khi hình dạng đầy đủ của hàm phân phối dữ liệu có thể không được biết và do đó ước tính khả năng tối đa không được áp dụng.
Phương pháp yêu cầu một số điều kiện nhất định được chỉ định cho mô hình. Các điều kiện thời điểm này là các hàm của các tham số mô hình và dữ liệu, sao cho kỳ vọng của chúng bằng 0 tại các giá trị thực của tham số. Phương pháp GMM sau đó tối thiểu hóa một chỉ tiêu nhất định của trung bình mẫu của các điều kiện thời điểm và do đó có thể được coi là một trường hợp đặc biệt của ước tính khoảng cách tối thiểu .
Các công cụ ước tính GMM được biết là nhất quán , bình thường không có triệu chứng và hiệu quả trong lớp của tất cả các công cụ ước tính không sử dụng bất kỳ thông tin bổ sung nào ngoài các điều kiện có trong điều kiện thời điểm.
GMM được phát triển bởi Lars Peter Hansen vào năm 1982 như là một khái quát của phương pháp khoảnh khắc , được giới thiệu bởi Karl Pearson vào năm 1894. Hansen đã chia sẻ giải thưởng Nobel về kinh tế năm 2013 một phần cho công việc này.
Biến công cụ là gì?
Ước tính các biến công cụ (IV) là cách tiếp cận gần như thí nghiệm nhằm khắc phục tính nội sinh thông qua việc sử dụng một công cụ hợp lệ. Ước tính IV là một phương pháp hữu ích trong phân tích dữ liệu để ước lượng nhất quán tác động nhân quả khi có các biến bị bỏ qua, sai số đo hoặc tính đồng thời giữa kết quả (Y) và biến quan tâm giải thích (X). Trang này cung cấp một cái nhìn tổng quan về ước tính và giả định IV. Để biết thêm chi tiết kỹ thuật về việc thực hiện, xem Tài nguyên bổ sung .
Một công cụ hợp lệ phải đáp ứng cả các điều kiện liên quan và ngoại sinh. Điều kiện liên quan nêu rõ rằng công cụ này có tương quan với biến quan tâm giải thích (X). Điều kiện ngoại sinh nói rằng thiết bị không tương thích với thuật ngữ lỗi (e). Nói cách khác, công cụ chỉ ảnh hưởng đến kết quả (Y) thông qua X. Để ước tính tác động nhân quả với biến công cụ, các nhà nghiên cứu có thể sử dụng bình phương tối thiểu hai giai đoạn (2SLS), phương pháp tổng quát về khoảnh khắc (GMM) hoặc ước lượng k.
Biến nội sinh là gì ?
Trong kinh tế lượng , tính nội sinh rộng rãi đề cập đến các tình huống trong đó một biến giải thích có tương quan với thuật ngữ lỗi . Sự khác biệt giữa các biến nội sinh và biến ngoại sinh bắt nguồn từ các mô hình phương trình đồng thời , trong đó người ta tách các biến có giá trị được xác định bởi mô hình từ các biến được xác định trước; bỏ qua tính đồng thời trong ước lượng dẫn đến ước tính sai lệch vì nó vi phạm giả định ngoại sinh của định lý Gauss Hồi Markov. Thật không may, vấn đề nội sinh là không may, đôi khi bị các nhà nghiên cứu tiến hành nghiên cứu phi thực nghiệm bỏ qua và không thực hiện các khuyến nghị chính sách. Các kỹ thuật biến công cụ thường được sử dụng để giải quyết vấn đề này.
Bên cạnh đó đồng thời, mối tương quan giữa các biến giải thích và thời hạn lỗi có thể phát sinh khi một không quan sát hoặc biến bỏ qua được nhiễu cả hai biến độc lập và phụ thuộc, hoặc khi biến độc lập được đo bằng lỗi .
Ước lượng GMM trên Eviews
Ta có mô hình nghiên cứu, ví dụ sau để ước lượng GMM trên Eviews:
lnp = eps + bvps + roe
Ta chọn lần lượt 4 biến trên theo thứ tự trên, đồng thời mở theo dạng Equation, đồng thời ta chọn method là gmm, và bấm vào mục Dynamic Panel Wizard, như hình bên dưới
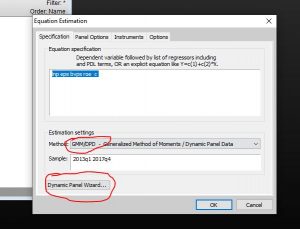
Nó sẽ hiện ra bảng tự động với 6 bước để thực hiện ước lượng gmm
- Bước 1: nó thông báo chúng ta là biến phụ thuộc đúng chưa, đồng thời nó chọn lag mặc định là 1, chúng ta có thể đổi lag, nhưng các bạn nên để lag mặc định như yêu cầu
- Bước 2 : Chúng ta để mặc định và bấm next ( Ước lượng các giai đoạn thơi gian, thông thường trong mô hình gmm họ không quan tâm đến, nếu các bạn muốn thì check vào mục: include period dummy variables
- Bước 3: Ta lại tiêp tục để mặc định ( Vì chúng ta sử dụng phương pháp ước lượng gmm là D.GMM)
- Bước 4: Nó đã tạo cho chúng ta 1 biến nội sinh mặc định, nên chúng ta bấm next. ( Nếu bạn biết chắc có một biến nội sinh nào khắc trong mô hình, thì bạn đưa vào lúc này cũng được)
- Bước 5: Các bạn để mặc định và bấm next
- Bước 6: Bạn chọn GMM interation: 2-step và GMM weighting matrix: White period. Bấm next để hoàn thành.
Bây giờ, thì phần mềm đã tự cấu hình cho chúng ta rồi, nên các bạn chỉ cần bấm OK cho Eviews tính toán kết quả nữa là xong.
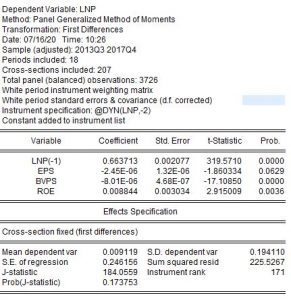
Các kiểm định cần thiết
Lượng biến công cụ hợp lí
Trong kết quả trên chúng ta có lượng biến công cụ là 171 trong khi đó, nhóm trong dữ liệu panel là 207. Như vậy lượng biến công cụ sinh ra là ít hơn lượng nhóm đối tượng trong dữ liệu panel. Nên ta có lượng đối biến công cụ trong mô hình là hợp lí. Như vậy kết quả ước lượng gmm để khắc phục nội sinh là phù hợp.
J-statistic test
Ta có Pvalue j-stat là 0.17 > 0.05
Ta đặt giả thuyết như sau:
- H0: Mô hình có hiện tượng nội sinh
- H1: Mô hình không có hiện tượng nội sinh
Cái kiểm định này gần giống Sargan test hay Hansen test trong Stata hay R …
Từ kết quả trên chúng ta chấp nhận H0, tức là mô hình có hiện tượng nội sinh.
Arellano Bond test
Đây là kiểm định tương quan chuỗi của Arellano Bond, cũng là một kiểm định rất quan trọng như 2 kiểm định trên, đáng lý tôi phải xếp kiểm định này lên đầu tiên, nhưng lỡ rồi tôi sẽ để nó thứ 3, thực chất là nó quan trọng bậc nhất trong mô hình hồi quy gmm này.
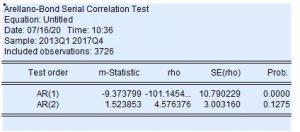
Ta có giả thuyết như sau:
- H0: Mô hình không có hiện tượng tự tương quan chuỗi
- H1: Mô hình có hiện tượng tương quan chuỗi
Tại AR(2) ta có Pvalue > 0.05, nên ta chấp nhận H0 bác bỏ H1, tức là mô hình không có hiện tượng tương quan chuỗi Arellano Bond.
Sau khi chúng ta kiểm định 3 việc trên thì kết quả cho ra là đáng tin cậy, vì vậy chúng ta có thể sử dụng được kết quả ước lượng gmm trong trường hợp này.
Nếu các bạn có bất kỳ khó khăn nào, các bạn đừng ngần ngại hãy liên với chúng tôi để được tư vấn miễn phí.




















0 nhận xét:
Đăng nhận xét