Dự báo Arima là gì ?
Dự báo ARIMA (ARIMA forecasts) là những kết quả dự báo được tạo ra từ mô hình dãy số thời gian của số bình quân trượt tích hợp tự tương quan (viết tắt từ chữ cái đầu của Autoregressive Integrated Moving Average).
Những mô hình thuộc loại này được thiết lập trên cơ sở nắm bắt tất cả các đặc trưng trong dãy số thời gian của một biến số (như xu thế, tính chất chu kỳ và các yếu tố có tính hệ thống khác) bằng cách gắn giá trị hiện tại của nó với các giá trị trễ của chính nó theo nhiều cách khác nhau.
George Box và Gwilym Jenkins (1976) đã nghiên cứu mô hình ARIMA và tên của họ thường được dùng dể gọi tên các quá trình ARIMA tổng quát, áp dụng vào việc phân tích và dự báo các chuỗi thời gian. Phương pháp Box-Jenkins với bốn bước: nhận dạng mô hình thử nghiệm, ước lượng, kiểm định bằng chẩn đoán, và dự báo.
Trên đây là khái niệm về dự báo arima,các bạn cũng chẳng cần nhớ để làm gì ? Các bạn chỉ cần nhớ dự báo ARIMA là kết hợp 3 mô hình riêng lẻ: p + d + q ( Thực ra chúng ta cần phải tìm các chỉ số này)
Mô hình Tự hồi quy Autogresssive (AR – p)
Trong thống kê , toán kinh tế và xử lý tín hiệu , một autoregressive ( AR ) mô hình là một đại diện của một loại quá trình ngẫu nhiên ; như vậy, nó được sử dụng để mô tả các quá trình thay đổi thời gian nhất định trong tự nhiên , kinh tế , v.v … Mô hình tự phát chỉ định rằng biến đầu ra phụ thuộc tuyến tính vào các giá trị trước đó của nó và vào một thuật ngữ ngẫu nhiên (thuật ngữ không thể dự đoán được); do đó mô hình ở dạng phương trình sai phân ngẫu nhiên(hoặc quan hệ lặp lại không nên nhầm lẫn với phương trình vi phân). Cùng với mô hình (MA) di chuyển trung bình , đó là một trường hợp đặc biệt và thành phần quan trọng của tổng quát hơn autoregressive chuyển động trung bình (ARMA) và tự hồi quy tích hợp trung bình trượt (ARIMA) mô hình chuỗi thời gian , trong đó có một ngẫu nhiên phức tạp hơn kết cấu; nó cũng là một trường hợp đặc biệt của mô hình tự phát vectơ (VAR), bao gồm một hệ thống gồm nhiều hơn một phương trình khác biệt ngẫu nhiên lồng vào nhau trong hơn một biến ngẫu nhiên đang phát triển.
Sai phân ( d)
Sai phân là làm cho dữ liệu của chúng ta dừng – ổn định không có xu hướng. ( Vì trong dữ liệu kinh tế, dữ liệu không có xu hướng thì ước lượng sẽ chính xác hơn).
Mô hình trung bình trượt ( Moving-Average: MA-q)
Trong phân tích chuỗi thời gian , mô hình trung bình di chuyển ( mô hình MA ), còn được gọi là quá trình trung bình di chuyển , là một cách tiếp cận phổ biến để mô hình chuỗi thời gian đơn biến . Mô hình trung bình di chuyển xác định rằng biến đầu ra phụ thuộc tuyến tính vào các giá trị hiện tại và quá khứ khác nhau của một thuật ngữ ngẫu nhiên (không hoàn toàn có thể dự đoán được).
Cùng với mô hình tự phát (AR) , mô hình trung bình di động là trường hợp đặc biệt và thành phần chính của các mô hình ARMA và ARIMA tổng quát hơn của chuỗi thời gian , có cấu trúc ngẫu nhiên phức tạp hơn.
Để dự báo mô hình ARIMA chúng ta cần tìm 3 số quan trọng là p + d + q, nó tương đương với AR(p) I(d) MA(q) trong mô hình dự báo Box-Jenkins. Trong khái niệm trên họ đề xuất 4 bước để thực hiện ước lượng và dự báo, nhưng trong bài thực hành này chúng tôi cũng dự báo bằng 4 bước, nhưng nội dung của từng bước là hoàn toàn khác biệt.
Thực hành dự báo ARIMA tự động
Đề tài:
Chúng tôi có một dữ liệu về chỉ số VNINDEX từ 09/12/2019 đến 24/04/2010, chúng ta cần dự báo thêm 10 ngày đến 08/05/2020. Trong dữ liệu này chúng tôi không dùng chỉ số VN-Index và dùng mức tăng trưởng của VN-Index để dự báo, mục đích là để nhìn vào thấy dấu âm hay dương là biết ngay ngày đó chỉ số vn-index tăng hay giảm so với ngày trước đó. Để biết những thông tin này, các bạn nên chạy thống kê mô tả trước khi phân tích dữ liệu bất kỳ, để hiểu rõ hơn về dữ liệu của mình.
Tìm p q d tự động trong R
Trong R có hàm auto.arima() trong gói forecast để tìm ra 3 chỉ số quan trọng đó rất nhanh, chúng ta chạy lệnh trên và có kết quả như sau:
auto.arima(dulieu$DVN)
## Series: dulieu$DVN
## ARIMA(4,0,3) with zero mean
##
## Coefficients:## Warning in sqrt(diag(x$var.coef)): NaNs produced
## ar1 ar2 ar3 ar4 ma1 ma2 ma3
## -0.9159 -0.0062 0.4862 -0.1057 1.1745 0.2718 -0.3855
## s.e. NaN NaN NaN NaN NaN NaN NaN
##
## sigma^2 estimated as 0.0001132: log likelihood=1033.89
## AIC=-2051.78 AICc=-2051.34 BIC=-2021.39Chúng ta liền có kết quả
- p=4
- d=0
- q=3
Kết quả trên thì dữ liệu đã dừng ở bậc gốc ( d=0), chúng ta có 4 lag phù hợp cho mô hình tự hồi quy AR(p) và có 3 lag phù hợp cho mô hình trung bình trượt MA(q).
Tìm lag phù hợp nhất
Như chúng ta đã biết với số lag trên thì chúng ta phải chọn lựa một mô hình arima tốt nhất trong 20 model con đó. Thông thường thì chúng ta sẽ hồi quy 20 lần để lựa chọn mô hình tốt nhất theo chỉ số AIC, Trong R chúng ta dùng một đoạn code ngắn gọn cho vòng lặp,thì chúng ta có kết quả như sau:
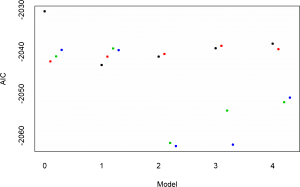
Kết quả chọn model:
## Model AIC
## 1 0.0 -2030.421
## 2 0.1 -2042.324
## 3 0.2 -2041.115
## 4 0.3 -2039.614
## 5 1.0 -2043.169
## 6 1.1 -2041.222
## 7 1.2 -2039.234
## 8 1.3 -2039.665
## 9 2.0 -2041.223
## 10 2.1 -2040.581
## 11 2.2 -2061.786
## 12 2.3 -2062.514
## 13 3.0 -2039.223
## 14 3.1 -2038.603
## 15 3.2 -2054.045
## 16 3.3 -2062.161
## 17 4.0 -2038.113
## 18 4.1 -2039.398
## 19 4.2 -2052.046
## 20 4.3 -2050.968Dựa vào chỉ số AIC nhỏ nhất ta được model thứ 12 với p=2 và q=3, nhưng vậy mô hình chúng ta đi ước lượng và dự báo như sau: AR(2)I(0)MA(3). Chúng ta có thể dựa báo trên R luôn, nhưng chúng ta sử dụng phần mềm Grelt để ước lượng và dự báo vì tính đơn giản và trực quan của nó.
Ước lượng ARIMA trên Grelt
Chạy dự báo ta được kết quả như sau:

Kết quả cho ước lượng tại lag bằng 1 and 2 mô hình Tự hồi quy đều có ý nghĩa thống kê, và tại lag bằng 1, 2, 3 cũng điều có ý nghĩa thống kê. bây giờ thì chúng ta đi dự báo thôi.
Dựa báo ARIMA trên Grelt
Bây giờ chúng ta dự báo thêm 10 ngày nữa, xem chỉ số VN-index như thế nào?. ta có kết quả như sau:
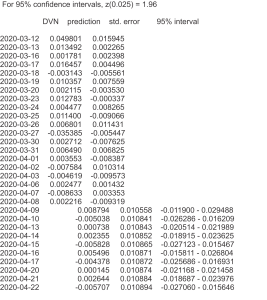
Kết quả dự báo 10 ngày tiếp theo từ 09/04 đến 22/04 có 6 ngày tăng và 4 ngày giảm.
Trên đây là chúng tôi thực hiện 4 bước để dự báo kết quả chỉ số VN-index.



















0 nhận xét:
Đăng nhận xét